HPC - One-dimensional coupled oscillators

Let us consider \(n\) points of mass \(m\) arranged along a straight line at coordinates \(x_0, x_1, \ldots, x_{n-1}\). Adjacent masses are connected by a spring with elastic constant \(k\) and rest length \(L\). The first and last points (those in position \(x_0\) and \(x_{n-1}\) occupy a fixed position and cannot move.

Initially, one of the springs is displaced so that a wave of oscillations is triggered; due to the lack of friction, such oscillations will go on indefinitely. Using Newton’s second law of motion \(F = ma\) and Hooke’s law which states that a spring with elastic parameter \(k\) that is compressed by \(\Delta x\) exerts a force \(k \Delta x\), we develop a program that, given the initial positions and velocities, computes the positions and speeds of all masses at any time \(t > 0\). The program is based on an iterative algorithm that, from positions and speeds of the masses at time \(t\), determine the new positions and velocities at time \(t + \Delta t\). In particular, the function

step(double *x, double *v, double *xnext, double *vnext, int n)

computes the new position xnext[i] and velocity vnext[i] of mass \(i\) at time \(t + \Delta t\), \(0 \le i < n\), given the current position x[i] and velocity v[i] at time \(t\).

1. For each \(i = 1, \ldots, n-2\), the force \(F_i\) acting on mass \(i\) is \(F_i := k \times (x_{i-1} -2x_i + x_{i+1})\); note that the force does not depend on the length \(L\) of the spring at rest. Masses 0 and \(n-1\) are stationary, therefore the forces acting on them are not computed.

2. For each \(i = 1, \ldots, n-2\) the new velocity \(v'_i\) of mass \(i\) at time \(t + \Delta t\) is \(v'_i := v_i + (F_i / m) \Delta t\). Again, masses 0 and \(n-1\) are statioary, therefore their velocities are always zero.

3. For each \(i = 1, \ldots, n-2\) the new position \(x'_i\) of mass \(i\) at time \(t + \Delta t\) is \(x'_i := x_i + v'_i \Delta t\). Masses 0 and \(n-1\) are stationary, therefore their positions at time \(t + \Delta t\) are the same as those at time \(t\): \(x'_0 := x_0\), \(x'_{n-1} := x_{n-1}\).

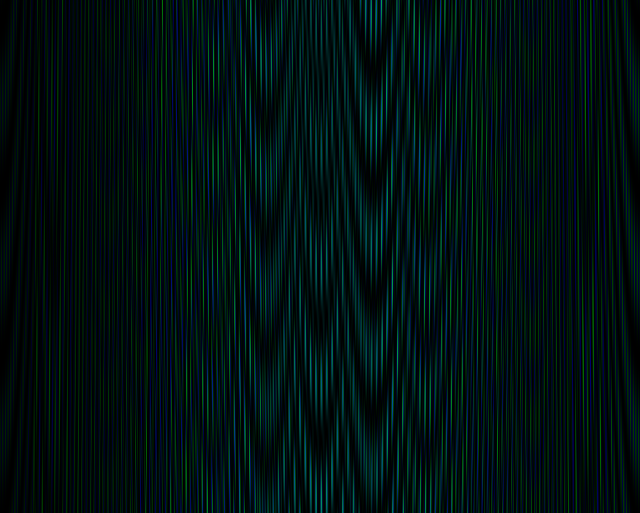
The file cuda-coupled-oscillators.cu contains a serial program that computes the evolution of \(n\) coupled oscillators. The program produces a two-dimensional image coupled-oscillators.ppm where each line shows the potential energies of the springs at any time (Figure 2).

Your task is to parallelize function step() by defining additional CUDA kernel(s).

To compile:

    nvcc cuda-coupled-oscillators.cu -o cuda-coupled-oscillators -lm

To execute:

    ./cuda-coupled-oscillators [N]

Example:

    ./cuda-coupled-oscillators 1024

Files

• cuda-coupled-oscillators.cu
• hpc.h